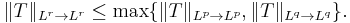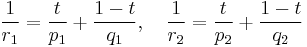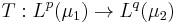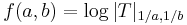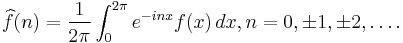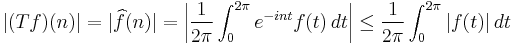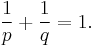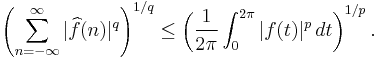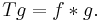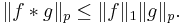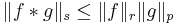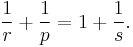Riesz–Thorin theorem
In mathematics, the Riesz–Thorin theorem, often referred to as the Riesz–Thorin interpolation theorem or the Riesz–Thorin convexity theorem is a result about interpolation of operators. It is named after Marcel Riesz and his student G. Olof Thorin.
This theorem bounds the norms of linear maps acting between Lp spaces. Its usefulness stems from the fact that some of these spaces have rather simpler structure than others. Usually that refers to L2 which is a Hilbert space, or to L1 and L∞. Therefore one may prove theorems about the more complicated cases by proving them in two simple cases and then using the Riesz–Thorin theorem to pass from the simple cases to the complicated cases. The Marcinkiewicz theorem is similar but applies to non-linear maps.
Contents |
Definition
A slightly informal version of the theorem can be stated as follows:
- Theorem: Assume T is a bounded linear operator from Lp to Lp and at the same time from Lq to Lq. Then it is also a bounded operator from Lr to Lr for any r between p and q.
This is informal because an operator cannot formally be defined on two different spaces at the same time. To formalize it we need to say: let T be a linear operator defined on a family F of functions that is dense in both 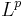 and
and 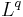 (for example, the family of all simple functions). And assume that Tƒ is in both
(for example, the family of all simple functions). And assume that Tƒ is in both 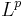 and
and 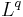 for any ƒ in F, and that T is bounded in both norms. Then for any r between p and q we have that F is dense in
for any ƒ in F, and that T is bounded in both norms. Then for any r between p and q we have that F is dense in 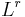 , that Tƒ is in
, that Tƒ is in 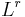 for any ƒ in F and that T is bounded in the
for any ƒ in F and that T is bounded in the 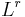 norm. These three ensure that T can be extended to an operator from
norm. These three ensure that T can be extended to an operator from 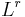 to
to 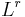 .
.
In addition an inequality for the norms holds, namely
A version of this theorem exists also when the domain and range of T are not identical. In this case, if T is bounded from 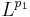 to
to 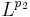 then one should draw the point
then one should draw the point 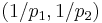 in the unit square. The two q-s give a second point. Connect them with a straight line segment and you get the r-s for which T is bounded. Here is again the almost formal version
in the unit square. The two q-s give a second point. Connect them with a straight line segment and you get the r-s for which T is bounded. Here is again the almost formal version
Theorem: Assume T is a bounded linear operator from 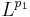 to
to 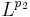 and at the same time from
and at the same time from 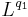 to
to 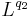 . Then it is also a bounded operator from
. Then it is also a bounded operator from 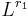 to
to 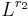 with
with
and t is any number between 0 and 1.
The perfect formalization is done as in the simpler case.
One last generalization is that the theorem holds for 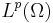 for any measure space Ω. In particular it holds for the
for any measure space Ω. In particular it holds for the 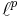 spaces.
spaces.
Convexity
Another more general form of the theorem is as follows (Dunford & Schwartz 1958, §VI.10.11). Suppose that μ1 and μ2 are two measures on possibly different measure spaces. Let T be a linear mapping from the space of μ1-integrable functions into the space of μ2-measurable functions, and for 1 ≤ p,q ≤ ∞, define 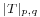 to be the operator norm of a continuous extension of T to
to be the operator norm of a continuous extension of T to
if such an extension exists, and ∞ otherwise. Then the theorem asserts that the function
is convex in the rectangle (a,b) ∈ [0,1]×[0,1].
Application examples
Hausdorff−Young inequality
We consider the Fourier operator, namely let T be the operator that takes a function  on the unit circle and outputs the sequence of its Fourier coefficients
on the unit circle and outputs the sequence of its Fourier coefficients
Parseval's theorem shows that T is bounded from 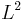 to
to 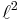 with norm 1. On the other hand, clearly,
with norm 1. On the other hand, clearly,
so T is bounded from 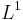 to
to 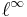 with norm 1. Therefore we may invoke the Riesz–Thorin theorem to get, for any 1 < p < 2 that T, as an operator from
with norm 1. Therefore we may invoke the Riesz–Thorin theorem to get, for any 1 < p < 2 that T, as an operator from 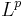 to
to 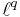 , is bounded with norm 1, where
, is bounded with norm 1, where
In a short formula, this says that
This is the Hausdorff–Young inequality.
Convolution operators
Let f be a fixed integrable function and let T be the operator of convolution with f, i.e., for each function g we have
It is well known that T is bounded from 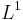 to
to 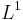 and it is trivial that it is bounded from L∞ to L∞ (both bounds are by
and it is trivial that it is bounded from L∞ to L∞ (both bounds are by 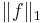 ). Therefore the Riesz–Thorin theorem gives
). Therefore the Riesz–Thorin theorem gives
We take this inequality and switch the role of the operator and the operand, or in other words, we think of S as the operator of convolution with g, and get that S is bounded from 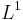 to
to 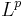 . Further, since g is in
. Further, since g is in 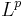 we get, in view of Hölder's inequality, that S is bounded from
we get, in view of Hölder's inequality, that S is bounded from 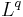 to L∞, where again
to L∞, where again 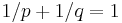 . So interpolating we get
. So interpolating we get
where the connection between p, r and s is
Thorin's contribution
The original proof of this theorem, published in 1926 by Marcel Riesz, was a long and difficult calculation. Riesz' student G. Olof Thorin subsequently discovered a far more elegant proof and published it in 1939. The English mathematician J. E. Littlewood once enthusiastically referred to Thorin's proof as "the most impudent idea in mathematics".
Here is a brief sketch of that proof:
One of its main ingredients is the following rather well known result about analytic functions. Suppose that 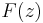 is a bounded analytic function on the two lines
is a bounded analytic function on the two lines 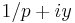 and
and 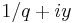 and on the strip between these two lines. Suppose also that
and on the strip between these two lines. Suppose also that 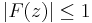 at every point
at every point  on those two lines. Then, by applying the Phragmén–Lindelöf principle (a kind of maximum principle for infinite domains) one gets that
on those two lines. Then, by applying the Phragmén–Lindelöf principle (a kind of maximum principle for infinite domains) one gets that 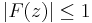 at every point between these two lines, and in particular at the point
at every point between these two lines, and in particular at the point 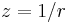 .
.
Thorin ingeniously defined a special analytic function  connected with the operator
connected with the operator  . He used the fact that
. He used the fact that  is bounded on
is bounded on 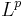 to deduce that
to deduce that 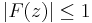 on the line
on the line 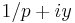 , and, analogously, he used the boundedness of
, and, analogously, he used the boundedness of  on
on 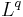 to deduce that
to deduce that 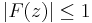 on the line
on the line 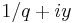 . Then, after using the result mentioned above to give that
. Then, after using the result mentioned above to give that 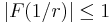 , he was able to show that this implies that
, he was able to show that this implies that  is bounded on
is bounded on 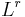 .
.
Thorin obtained this function  with the help of a generalized notion of an analytic function whose values are elements of
with the help of a generalized notion of an analytic function whose values are elements of 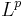 spaces instead of being complex numbers. In the 1960s Alberto Calderón adapted and generalized Thorin's ideas to develop the method of complex interpolation. Suppose that
spaces instead of being complex numbers. In the 1960s Alberto Calderón adapted and generalized Thorin's ideas to develop the method of complex interpolation. Suppose that 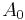 and
and 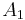 are two Banach spaces which are continuously contained in some suitable larger space. Calderon's method enables one to construct a family of new Banach spaces
are two Banach spaces which are continuously contained in some suitable larger space. Calderon's method enables one to construct a family of new Banach spaces 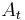 , for each
, for each  with
with 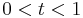 which are ``between"
which are ``between" 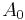 and
and 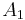 and have the ``interpolation" property that every linear operator
and have the ``interpolation" property that every linear operator  which is bounded on
which is bounded on 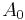 and on
and on 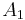 is also bounded on each of the complex interpolation spaces
is also bounded on each of the complex interpolation spaces 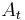 .
.
Calderon's spaces have many applications. See for example Sobolev space.
Mityagin's theorem
B.Mityagin extended the Riesz–Thorin theorem; we formulate the extension in the special case of spaces of sequences with unconditional bases (cf. below).
Assume 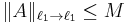 ,
, 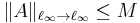 . Then
. Then 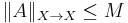 for any unconditional Banach space of sequences
for any unconditional Banach space of sequences  (that is, for any
(that is, for any 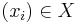 and any
and any 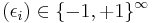 ,
, 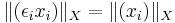 ).
).
The proof is based on the Krein–Milman theorem.
References
- Dunford, N.; Schwartz, J.T. (1958), Linear operators, Parts I and II, Wiley-Interscience.
- Glazman, I.M.; Lyubich, Yu.I. (1974), Finite-dimensional linear analysis: a systematic presentation in problem form, Cambridge, Mass.: The M.I.T. Press. Translated from the Russian and edited by G. P. Barker and G. Kuerti.
- Hörmander, L. (1983), The analysis of linear partial differential operators I, Grundl. Math. Wissenschaft., 256, Springer, ISBN 3-540-12104-8, MR0717035.
- Mitjagin [Mityagin], B.S. (1965), "An interpolation theorem for modular spaces (Russian)", Mat. Sb. (N.S.) 66 (108): 473–482.
- Thorin, G. O. (1948), "Convexity theorems generalizing those of M. Riesz and Hadamard with some applications", Comm. Sem. Math. Univ. Lund [Medd. Lunds Univ. Mat. Sem.] 9: 1–58, MR0025529